function [signal] = project_01_part04b(f0, fs, secs, velocity, dist_from_track, observer_distance)

%comment out f0, fs, secs, velocity, dist_from_track, and observer_distance
%to specify values from command line
c = 340;                    %speed of sound
velocity = 10;              %velocity of sound source
f0 = 220;                   %center frequency of sound
fs = 8000;                  %sampling frequency
secs = 10;                  %duration of sound
dist_from_track = 5;        %shortest distance from observer to track
observer_distance = 0.17;   %17 cm is distance between adult human ears

time = -secs/2:1/fs:secs/2;
x(1,:) = velocity*time-observer_distance/2; %x-component of distance to sound source on track
x(2,:) = velocity*time+observer_distance/2; %x-component of distance to sound source on track

hypo = zeros(2,length(time));
%change in hypotenuse equals relative distance from sound source to observer
for i = 1:size(hypo,1)*length(hypo)
    hypo(i) = sqrt((x(i))^2 + dist_from_track^2);
end

env = 1./abs(hypo);
%velocity relative to observer is orig velocity vector * adj/hypo (cosine)
vel_rel_observer = velocity*x./hypo;

f = zeros(2,length(time));
%here size(f,1) returns 2 - can run thru entire 2 row matrix this way
for i = 1:size(f,1)*length(f)
    f(i) = f0*(c/(c+vel_rel_observer(i)));
end

%sort of complicated way to create the stereo signal..
signal(:,1) = env(1,:).*sin(2*pi*f(1,:).*time);
signal(:,2) = env(2,:).*sin(2*pi*f(2,:).*time);

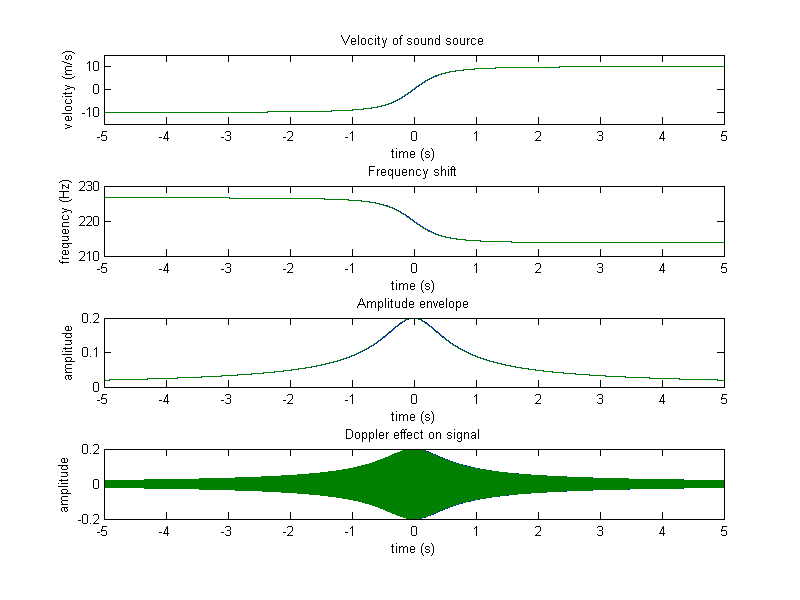
subplot(411), plot(time,vel_rel_observer), axis([min(time),max(time),-1.5*velocity,1.5*velocity]);
title('Velocity of sound source'), xlabel('time (s)'), ylabel('velocity (m/s)');
subplot(412), plot(time,f);
title('Frequency shift'), xlabel('time (s)'), ylabel('frequency (Hz)');
subplot(413), plot(time,env);
title('Amplitude envelope'), xlabel('time (s)'), ylabel('amplitude');
subplot(414), plot(time,signal);
title('Doppler effect on signal'), xlabel('time (s)'), ylabel('amplitude');

%double max(max()) needed, because max() on a matrix returns a row vector
signal = signal/max(max(abs(signal)));

%print project_01_part04b -dpng -r100;
%wavwrite(signal,fs,'project_01_part04b');

soundsc(signal,fs);