Driving in City Squares 

The city AllSquared has been designed by many famous architects and engineers. The city lays in a retangular area of $n \times m$ squared miles (n refers to the retangle basis, and m to its height). The streets are horizontal divisions distributed uniformly at every one mile, and the avenues are vertical divisions also uniformly distributed at every one mile. Streets are numbered from north to south, starting from zero; avenues from west to east, also starting from zero.

The figure (a) below portrays the city layout for n = 11 and m = 8. The city is also

#1#2#3#4#5 @font#1#2pt #3#4#5

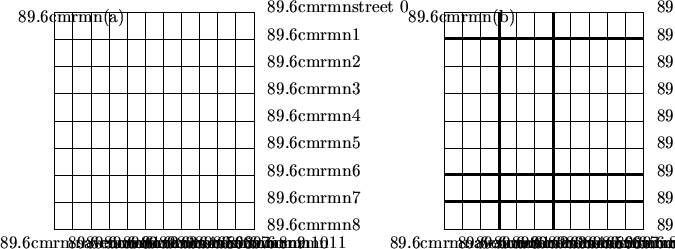
divided in horizontal and vertical strips, with the intersection of these strips defining the city subregions (counties). Figure (b) pictures a city divided into 12 counties.

Every county is associated with a vehicle circulation fee, which should be paid every time a car enters the county. If the car origin is a street or avenue delimiting the county, there is no fee. For example, in the above figure a car whose origin is street = 2 and avenue = 3 and whose target is street = 2 and avenue = 9 will have to pay only the county crossing fee relative to avenue 6.

You should write a program that has the following input:

• two strictly positive integers n and m specifying the city dimensions;
• two positive integers h and v specifying the number of horizontal and vertical strips, respectively (for the city in the figure, h = 4, v = 3);
• h - 1 integers $s_1, \dots, s_{h-1}$ ( $1 \le s_i \le n - 1$) which denote the streets in which there is a county division line (in the previous figure, the numbers are 1, 6, and 7);
• v - 1 integers $a_1, \dots, a_{v-1}$ ( $1 \le a_i \le m - 1$) which denote the avenues in which there is a county division line (in the the previous figure, the numbers are 3 and 6);
• the circulation fees for each county in the city, i.e., h * v positive real numbers
  
  $$\begin{array}{l} p_{11}, p_{12}, \dots, p_{1v} \\ p_{21}, p_... ... p_{2v} \\ \dots \\ p_{h1}, p_{h2}, \dots, p_{hv} \end{array}$$
  
  
  where p_ij is the circulation fee for the county delimited by ai-1 (west), a_i+1 (east), s_j-1 (north), and s_j+1 (south);
• two pairs of positive integers local₁ = (str₁, av₁) e local₂ = (str₂,av₂)

The output should be the smallest possible price to pay for going from local 1 to local 2 .

Input 

The input format may contain several instances of the problem. Each instance is terminated by a line starting with % (percentage symbol).

The description for one instance has the following format:

n	m
h	v
s1	s2	$\dots$	sh-1
a1	a2	$\dots$	av-1
p11	p12	$\dots$	p1v
p21	p22	$\dots$	p2v
$\dots$
ph1	ph2	$\dots$	phv
w1	t1	w2	t2
%

where

• n, m, h, v are integers such that $0 < n, 0 < m, 0 < h \le n, 0 < v \le m$;
• $s_1, \dots, s_{h-1}$ are such that $1 \le s_i \le n - 1$ for $1 \le i \le h - 1$;
• $a_1, \dots, a_{v-1}$ are such that $1 \le a_i \le m - 1$ for $1 \le v - 1$;
• p_ij are positive real numbers;
• w₁, t₁, w₂, t₂ are integers such that $0 \le w_1, w_2 \le n$ and $0 \le t_1, t_2 \le m$. (w₁, t₁) is the origin and (w₂, t₂) is the target point for the problem;
• there can be an arbitrary number of spaces or empty lines between the numbers in the file.

Output 

For an input file with k instances of the problem, the output file should follow the format:

c₁

c₂

$\dots$

c_k

where c_i is the result for the i^th instance in the input file.

Sample Input 

100 100
3 4
30 60
10 70 80
5 100 1 20
1 100 1 20
1 1 1 20
5 5 10 75
%
11 8
4 3
1 6 7
3 6
10 10 10
10 10 10
10 10 10
10 10 10
2 3 2 9
%

Sample Output 

6
10