A child has drawn N (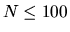 )
numbered circles of different colors.
He has connected some of the
circles by colored oriented line segments. Every pair of circles may have
any number of segments,
with any colors, connecting them. Each color (either circle color or segment
color) is assigned its
own unique positive integer number not greater than 100.
)
numbered circles of different colors.
He has connected some of the
circles by colored oriented line segments. Every pair of circles may have
any number of segments,
with any colors, connecting them. Each color (either circle color or segment
color) is assigned its
own unique positive integer number not greater than 100.
Starting the game the child first of all chooses three different integers
L, K and Q within the range
between 1 and N. Then he places one pawn into the circle number L and
another one into the circle
number K, whereupon he begins to move them using the following rules:
- a pawn can be moved along the line segment, if this segment has the
same color with the
circle where another pawn is placed,
- the pawn can be moved only in the direction of the segment (all
segments are oriented),
- two pawns can never be placed in the same circle at the same time,
- the move order is free (i.e. it is not necessary to move pawns
alternately),
- the game ends, when one of the pawns (any of the two) reaches the
last circle number Q.
You are to write a program to find out the shortest (i.e. containing a
minimal number of moves)
solution for this game, if it exists.
The first line of the input file contains integers
N, L, K, Q separated
by spaces.
The second line
consists of N integers
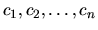 , separated by spaces,
in the given order,
where ci is the color of
the circle number i. The third line consists of a single integer M
(
, separated by spaces,
in the given order,
where ci is the color of
the circle number i. The third line consists of a single integer M
(
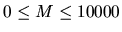 )
denoting the total
number of segments. Then follow M lines, each containing a description
of one oriented segment.
Each segment is described by three integer numbers
Aj, Bj, Cj, separated by spaces,
where A and B
are the numbers of the circles connected by the j-th segment with direction from Aj to Bj ,
and Cj represents the color of this segment.
)
denoting the total
number of segments. Then follow M lines, each containing a description
of one oriented segment.
Each segment is described by three integer numbers
Aj, Bj, Cj, separated by spaces,
where A and B
are the numbers of the circles connected by the j-th segment with direction from Aj to Bj ,
and Cj represents the color of this segment.
The first line of the output file should contain the word ``YES", if
the game can
come to the end, and ``NO" otherwise (without quotes). If the answer
is ``YES",
the second line of the output should contain just a single integer - the
minimum number of the
moves the child should make to finish the game.
5 3 4 1
2 3 2 1 4
8
2 1 2
4 1 5
4 5 2
5 1 3
3 2 2
3 2 4
5 3 1
3 5 1
YES
3
Miguel Revilla
2000-12-30
![]() )
numbered circles of different colors.
He has connected some of the
circles by colored oriented line segments. Every pair of circles may have
any number of segments,
with any colors, connecting them. Each color (either circle color or segment
color) is assigned its
own unique positive integer number not greater than 100.
)
numbered circles of different colors.
He has connected some of the
circles by colored oriented line segments. Every pair of circles may have
any number of segments,
with any colors, connecting them. Each color (either circle color or segment
color) is assigned its
own unique positive integer number not greater than 100.