Least Path Cost 

Given a positive integer $\Delta$ ( $0 < \Delta < 10000$), which is called the overhead, and M ( $0 < M \le 200$) straight line segments in a two-dimensional plane with the following properties:

1.

each line segment has a height, which is a positive integer;

2.

two line segments only intersect with each other on endpoints;

3.

no two line segments are overlapped.

Each line has a unique number between 1 and M. Each endpoint in the plane has a unique number between 1 and N ( $0 < N \le 400$), where N is the total number of endpoints. A line segment is represented by its two endpoints (n_i, n_j). Let height(L) be the height of a line segment L.

A path is a sequence of line segments $L_{C_1}, L_{C2}, \dots, L_{C_k}$, such that k > 1, $C_i \neq C_j \quad \forall i \neq j$, L_Ci intersects with L_C<<55>>i+1 for all $1 \le i < k$, one endpoint of L_C1 does not intersect with any other line segments, and one endpoint of L_Ck does not intersect with any other line segments. The cost between two intersection line segments i L_Ci and L_C<<59>>i+1 is

$$\left \vert height(L_{C_i}) - height(L_{C_{i+1}}) \right \vert$$

That is, for example you can image, the number of stairs that one has to climb (up or down ) by walking from L_Ci to L_C<<63>>i+1. The cost of a path $L_{C_1}, L_{C2}, \dots, L_{C_k}$ is

$$k \cdot \Delta + \sum_{i=1}^{k-1} cost(L_{C_i},L_{C_{i+1}}).$$

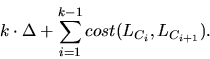
In the example shown in Fig. 1, $\Delta$ = 25, M = 8, and N = 9. Then cost(L₂, L₃) = 1 and cost(L₁, L₆ ) = 8. L₁, L₄, L₅ is not a path. There are three paths in the plane. The cost for the path L₁, L₆, L₇, L₈ is 109. The cost for the path L₁, L₄, L₅ ,L₈ is 131. The cost for the path L₂, L₃ is 51. Hence L₂, L₃ is the path with the least cost.

You may also assume there is at least one path in the plane. Write a program to find the least cost among all paths. 

Input 

The first line is l, the number of test cases. The first three lines of test case #i are M_i, N_i and $\Delta_i$ which are the numbers of line segments and endpoints, and the overhead, respectively. The following M_i lines each contains the two endpoints of each line segment, starting from L₁ to L_Mi, and its height.

Each line segment is represented by three integers, separated by blanks.

Output 

Contains l lines. The i^th line contains the least cost of all paths in the i^th test case.

Fig. 1: An example of 8 straight lines with 9 endpoints.

Sample Input 

2
8
9
25
1 2 1
8 9 10
7 8 9
1 4 2
4 5 20
1 3 9
3 5 9
5 6 8
6
6
21
1 2 1
1 4 2
4 5 20
1 3 9
3 5 9
5 6 8

Sample Output 

51
93