Convex Hull Finding 

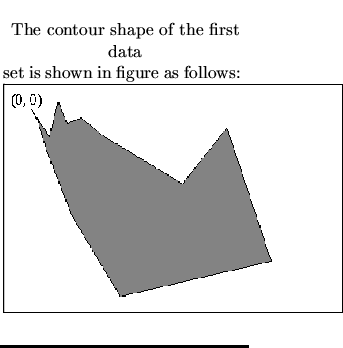
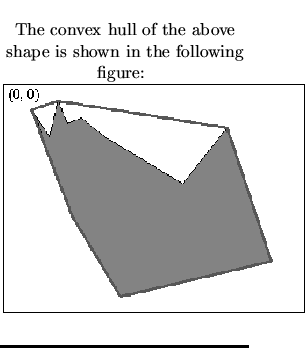
Given a single connected contour, which is either convex or non-convex (concave), use any algorithm to find its Convex Hull, i.e., the smallest convex contour enclosing the given shape. If the given contour is convex, then its convex hull is the original contour itself. The maximal size of the shape is 512$\times$512, and the maximal number of the vertices of the shape is 512. Write a program to read the input data (the given shapes) from a disk file, implement your convex hull finding algorithm, and then output the shape data of the results to the standard output.

Input 

The order of the vertices is counterclockwise in X-Y Cartesian Plane (if you consider the origin of the display window is on the upper-left corner, then the orientation of the vertices is clockwise), and none of the neighboring vertices are co-linear. Since all the shapes are closed contours, therefore, the last vertex should be identical to the first vertex. There are several sets of data within a given data file. The negative number -1 is used to separate the data set.

Line	Data in
Number	the File	Explanation
1	K	a positive integer showing how many sets of data in this file
2	N	a positive integer showing the number of vertices for the shape
3	$X_1 \ Y_1$	two positive integers for the first vertex (X1, Y1)
4	$X_2 \ Y_2$	two positive integers for the next neighboring vertex (X2, Y2)
...
N+2	$X_N \ Y_N$	two positive integers for the last vertex (XN, YN)
N+3	-1	Delimiter
N+4	M	a positive integer showing the number of vertices for the next shape
N+5	$XX_1 \ YY_1$	two positive integers for the first vertex
...

Note: Please note that the Line Number, Data in the File and Explanation are not given in the file. They are shown here only to assist you in reading the data.

Output 

Output the convex hull of all K input shapes to the standard output. The data format should be the same as the input file. In addition, the vertex with the smallest Y value should be the first point and if there are points with the same Y value, then the smallest X value within those points should be the first point.

Sample Input 

3
15
30 30
50 60
60 20
70 45
86 39
112 60
200 113
250 50
300 200
130 240
76 150
47 76
36 40
33 35
30 30
-1
12
50 60
60 20
70 45
100 70
125 90
200 113
250 140
180 170
105 140
79 140
60 85
50 60
-1
6
60 20
250 140
180 170
79 140
50 60
60 20

Sample Output 

3
8
60 20
250 50
300 200
130 240
76 150
47 76
30 30
60 20
-1
6
60 20
250 140
180 170
79 140
50 60
60 20
-1
6
60 20
250 140
180 170
79 140
50 60
60 20

$\parbox{.44\textwidth}{ \begin{center} The contour shape of the firs... ...n in figure as follows: \mbox{} \epsfysize 2in \epsfbox{p681.eps} \end{center}}$ $\parbox{.44\textwidth}{ \begin{center} The convex hull of the above ... ... the following figure: \mbox{} \epsfysize 2in \epsfbox{p681b.eps} \end{center}}$