Horse Step Maze 

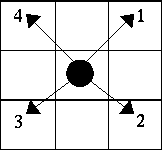
Maze search has been developed for a long time, and the related competition is held often. In this problem you have to design a program that simulates a computer mouse to find a path in a maze from a starting point to an ending point. To find such a path, the computer mouse must follow the `knight' steps as shown in Fig. 1. The numbers 1, 2, 3 and 4 indicate the sequence of four directions the computer mouse has to try while searching for a path. Specifically, the computer mouse must always try direction 1 first until it cannot continue searching the path to the ending point in the maze. When that happens, the computer mouse can backtrack and try direction 2. Similarly, if direction 2 can not work, direction 3 is tried and then direction 4.

Your program has to prevent the path to enter in a loop.

represents the location of computer mouse at present

represents the step that computer mouse can walk

The numbers 1, 2, 3 and 4 indicate the sequence of four directions the computer mouse must follow to find a path in the maze.

Fig. 1: The rule of the horse step

The size of given maze is 9 by 9, and its coordinates are shown in Fig. 2. Initially, you are given the starting and ending points of a maze. Your program must print the walking path of the mouse if the ending point of the maze can be reached and the number of steps is less than or equal to 50000. If the number of steps is over 50000 print `more than 50000 steps'. Otherwise, ``fail'' should be printed.

Fig. 2: The coordinates of the maze

Input 

The coordinate of the starting point followed by the coordinate of the ending point in a maze.

Output 

The coordinates of the walking path from the starting point to the ending point or ``fail''.

Sample Input 

(1,1)
(9,9)

Sample Output 

(1,1), (2,2), (1,3), (2,4), (1,5), (2,6), (1,7), (2,8), (1,9), (2,8), (3,9), (4,8), (5,9), (6,8), (7,9), (8,8), (9,9)