| Don't Get Hives From This One! |
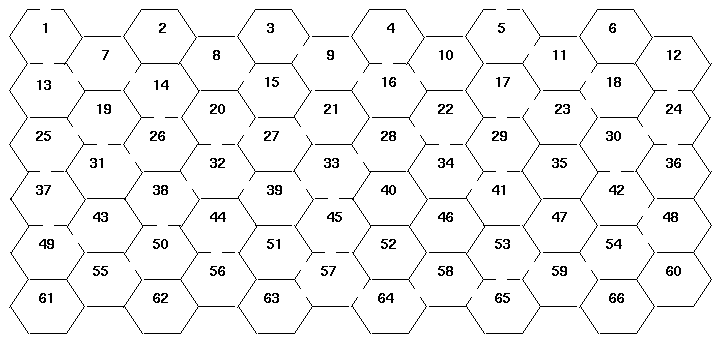
Billy Bee has big ideas. He wants to use an abandoned level of the beehive as a ``fun-house maze." The idea is to sell tickets and make big bucks. The sample below is ``rectangular" and has eleven rows and twelve columns. Billy's maze will also be rectangular, and similarly shaped, but might have different dimensions. The cells are identified by a sequence of numbers, starting with 1, in the pattern shown. The maze comes from the fact that many adjacent cells have openings between them. There are also two openings to the outside: an entrance and an exit.

You can assume that the cells in the maze are oriented as shown above (horizontal and slanted sides, but no vertical sides), and that the second row of the maze starts below and to the right of the first room in the maze.
Billy has already set up his maze, but he is not very smart and can't solve it for himself. He has hired you to help him find a path through his maze (or, if his maze has no solution, to inform him of the fact). In your own quest for big bucks, you decide to develop a computer program to solve such ``rectangular hexagonal mazes" by the well known right-hand rule and charge Billy Bee for the development costs. Then you'll turn around and sell the software to Bill Gates, hoping you don't get stung in the process.
The righthand rule states that, when you enter a planar maze, if you place your right hand on the entrance wall, and then walk forth, never removing the hand from the wall, you will eventually exit the maze through the exit door (or, if the exit is inaccessible, you will exit through the entrance door).
The input file will contain zero or more maze descriptions, immediately following one another.
The first line of each maze description will contain two positive integers, r and c, (r<=30, c<=30) separated by a space, indicating, respectively, the number of rows and columns in the maze. Alternatively, the line may contain just two zeroes, separated by a space, indicating that there are no more mazes to read and solve.
The second line of each maze description will also contain two positive integers, separated by a space, indicating the room number and wall number, respectively, of the maze's entrance. (Walls of each room are assumed to be numbered clockwise, starting from topwall=1.)
The third line will identify the room number and wall number of the maze's exit in the same manner. The entrance and exit to the maze are different doors.
The remaining lines each describe a room in the maze. Each of these lines contains a room number, followed by from one to six integers, each in the range 1 to 6, inclusive, separated by single spaces. The integers following the room numbers indicate the walls containing openings, and may be in any order, as may be the lines themselves. Rooms will not be repeated in a data set. Rooms not listed in a data set have no doors (for example, room 60 in the sample data).
The end of the maze description is indicated by a line containing only the integer 0. The line after that either begins the next maze description, or contains the two zeroes that indicate the end of data.
Your program may assume the data to be valid and consistent. The maze shown in the picture would be described using the following Sample Input data.
First, the program should list the sequence of rooms encountered during the search for a solution, twenty rooms per line (except possibly the final line), with values on the same line separated by a single space. Note that the last room listed will either be the exit room (if a solution was found) or the entrance room (otherwise).
Second, the line immediately below the final line of the search path should contain either the phrase SOLUTION FOUND or else the phrase NO SOLUTION, corresponding to whether or not a path from the entrance to the exit was found.
11 12 1 1 5 1 1 1 4 56 1 57 1 3 5 6 58 3 5 3 3 11 3 6 12 4 13 1 2 14 4 6 15 6 16 1 2 6 17 3 4 18 5 6 19 4 5 2 3 4 21 5 22 4 5 23 2 6 24 1 4 5 25 2 4 26 1 5 27 2 6 28 2 5 29 1 4 3 2 4 31 1 2 32 1 3 5 33 2 5 4 34 1 3 4 4 5 1 3 7 5 3 8 3 9 6 3 1 5 36 1 37 1 4 38 2 4 39 2 6 41 1 6 42 1 3 43 5 44 4 45 1 4 48 5 6 49 1 2 5 1 5 51 3 53 3 4 54 2 5 55 2 59 2 6 63 2 64 2 6 65 1 6 0 0 0
1 13 7 14 26 31 19 25 37 49 43 49 37 25 19 31 26 14 7 13 1 NO SOLUTION