Problem C
The Stern-Brocot Number System
Input: standard input
Output: standard output
The Stern-Brocot tree is a beautiful way for constructing the set of
all nonnegative fractions m / n where m and n are relatively
prime. The idea is to start with two fractions ![]() and then repeat the
following operations as many times as desired:
and then repeat the
following operations as many times as desired:
Insert ![]() between two adjacent
fractions
between two adjacent
fractions ![]() and
and ![]() .
.
For example, the
first step gives us one new entry between ![]() and
and ![]() ,
,
![]()
and the next gives two more:
![]()
The next gives four more,
![]()
and then we will get 8, 16, and so on. The entire array can be regarded as an infinite binary tree structure whose top levels look like this:
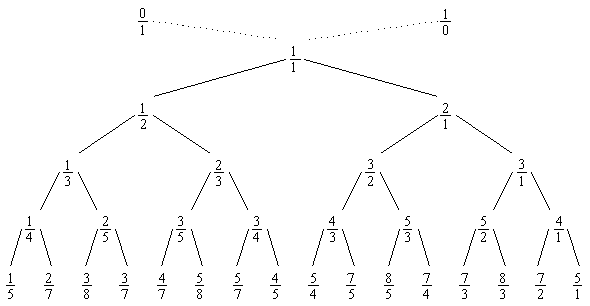
The construction preserves order, and we couldn't possibly get the same fraction in two different places.
We can, in fact,
regard the Stern-Brocot tree as a number system for representing rational
numbers, because each positive, reduced fraction occurs exactly once. Let's use
the letters L and R to stand for going down to the left or
right branch as we proceed from the root of the tree to a particular fraction;
then a string of L's and R's uniquely identifies a place in the
tree. For example, LRRL means that we
go left from ![]() down to
down to ![]() , then right to
, then right to ![]() , then right to
, then right to ![]() , then left to
, then left to ![]() . We can consider LRRL
to be a representation of
. We can consider LRRL
to be a representation of ![]() . Every positive fraction gets represented in this way as a
unique string of L's and R's.
. Every positive fraction gets represented in this way as a
unique string of L's and R's.
Well, actually
there's a slight problem: The fraction ![]() corresponds to the empty string, and we need a notation for
that. Let's agree to call it I,
because that looks something like 1 and it stands for "identity".
corresponds to the empty string, and we need a notation for
that. Let's agree to call it I,
because that looks something like 1 and it stands for "identity".
In this problem, given a positive rational fraction, you are expected to represent it in Stern-Brocot number system.
Input
The input file contains multiple test cases. Each test case consists of a line contains two positive integers m and n where m and n are relatively prime. The input terminates with a test case containing two 1's for m and n, and this case must not be processed.
Output
For each test case in the input
file output a line containing the representation of the given fraction in the Stern-Brocot number system.
Sample Input
5 7878 323
1 1
Sample Output
LRRLRRLRRLRLLLLRLRRR