1.

For this question, you are going to be working with a list of objects. The objects represent Very Large Numbers, but you do not need to be concerned with how they are implemented. The class declaration is given below, you do NOT need to define any part of the number class. The declarations of the member variables have been left out; do not be concerned with them.

Every object of type number occupies 75 bytes of memory.

class number

{ public:

number(void);

number(string s);

void add(number x);

void subtract(number x);

void multiply(number x);

void divide(number x);

int compare(number x);

void print(void); };

Using this class definition, if a and b are numbers, then a.add(b) performs the operation a+=b; and all the arithmetical operations work in the same way. a.compare(b) returns –1 if a is less than b, 0 if a is equal to b, and +1 if a is greater than b. The first constructor takes a string containing the normal decimal representation of an integer (e.g. "347821634") and makes a number from it.

Here are two declarations:

number AA[100];

number *BB[100];

Say, in plain English, exactly what each declaration declares, and how much memory each will occupy. List and explain the relative advantages and disadvantages (if any) of each declaration in terms of memory use, speed of execution, and convenience for programming.

AA is an array of 100 number objects, and occupies 7500 bytes.

BB is an array of 100 pointers to number objects, and under the safe assumption that pointers require 4 bytes, occupies 400 bytes.

If it is not known how many objects will be required, an array must be created at the maximum possible size, which can involve a lot of wasted memory. Using BB only wastes 4 bytes for each entry that turns out to be unnecessary, whereas AA wastes 75 bytes for each.

If putting things into the array, or moving array entries around, is to be a common operation then BB is faster, because only 4 bytes needs to be moved each time. If accessing components of the objects within the array is to be a common operation then AA is faster, because following a pointer does take some time.

AA requires the existence of a default constructor for number, and some mechanism for determining whether or not an array entry is in use. With BB, unused entries can be set to NULL.

The next part requires you to write three functions that work with the second declaration (BB). Think about all three before you start the first, as the design of each depends upon the designs of all. Your three functions must work together properly.

I would choose a design which uses an extra int variable to record how many entries in the array are in use. That way I would not need to spend any time setting all the entries of a potentially enormous array to NULL. Such a design would require me to ensure that no gaps are left in the array, so after removal an element will have to be repositioned to fill the gap left.

This design decision means that the result of find is in some way unstable. If I find a number, then remove another number, it might be that the first number found gets relocated as a result of the removal, so the position I’ve got for it becomes invalid. If this is unacceptable, a different design would be required.

Write three functions, one to add a number to the list stored in BB, one to search for a particular number in the list BB, and one to remove a particular number from BB. The prototypes for the functions are:

int addtolist(number *n); // returns 1 normally but 0 if it fails for some reason

int find(number *n); // returns the position in the list, or –1 if not found

int remove(number *n); // returns 1 normally, or 0 if it fails.

You may add extra functions or variables if necessary.

int num=0; // the number of entries in use.

const int max=100; // the maximum capacity.

int addtolist(number *n)

{ if (num>=max) return 0; // this is the only possible cause of failure

BB[num]=n;

Num+=1; }

int find(number *n)

{ for (int i=0; i<num; i+=1)

if (BB[i]->compare(*n)==0)

return i;

return -1; }

In the find function, notice that the normal comparison (BB[i]==n) is not good enough; it just compares the two pointers. We need to compare the actual number objects. It is possible that two number objects with different addresses in memory will contain the same number.

int remove(number *n)

{ int i=find(n); // no need to repeat the work

if (i==-1) return 0; // only reason for failure to remove is absence from list

num-=1;

BB[i]=BB[num]; } // move last number down to fill the gap

Finally, write a function with the following prototype:

int addinputtolist(void);

it waits for the user to type a number, and then adds it to the list BB, returning 1 for success, or 0 for failure.

The only useful constructor we have for a number is the one that takes a string parameter, so we have to read a string from the user, then convert it to a number. There are three very similar and equally correct ways of doing this. All three methods use “new number” to create the new number in permanent memory, so that it will still be valid when the function exits. All three functions also use the already defined function addtolist to avoid unnecessary duplication of effort and additional chances of error.

// using iostream

int addinputtolist(void)

{ string s;

cin >> s;

return addtolist(new number(s)); }

// using stdio

int addinputtolist(void)

{ char s[1000];

scanf(“%s”, s);

return addtolist(new number(s)); }

// using stdio in a probably more sensible way

int addinputtolist(void)

{ char s[1000];

fgets(s, 999, stdin);

int n=strlen(s);

if (s[n-1]==’\n’) s[n-1]=’\0’;

return addtolist(new number(s)); }

2.

A Queue is a special object for holding data. It behaves rather like an array, except that you are only allowed to access the data it contains in a very restricted way. Apart from constructors, there are usually only three simple access methods for a queue:

1. A checking method: is_empty(); returns 1 if the queue has no data in it, 0 otherwise.

2. An insertion method: insert(something *); adds the given object to the queue's collection of data.

3. A removal method: something *remove(void); removes an object from the queue, and returns that object as its result.

Notice that the only way to get information from the queue also involves permanently removing that piece of information, and there is no way to say which piece of information you want. That restriction is fundamental to queues.

The simple rule is that objects are removed in exactly the order they were inserted in. If you insert A then insert B then insert C, then remove something, you will get A back. If you then insert D then remove something, you get B back. If you then remove another thing you get C, and removing another thing gets D, after which the queue is empty again. Insertions and removals can be done at any time; a removal always gets the object that has been in the queue for longest.

An alternative, and perhaps better, way of thinking about a queue is to say that a queue has two ends, the front and the back. Objects can only be added to the back of a queue, and can only be removed from the front.

objects go in here objects come out here

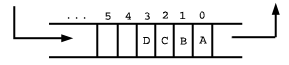
Implement a queue object (define the class and all appropriate constructors and methods) suitable for holding a queue of person objects. Do not worry about defining person, just assume that class already exists. Although the insert and remove methods may be used millions of times, you are assured that there will never be more than 100 objects in your queue at the same time (i.e. if insert has been used 1,000,000 times, you can be sure that remove has been used at least 999,900 times).

First, notice that you aren’t expected to know anything about queues in order to answer this question. Everything you need is given above.

An initial incorrect design will give the general idea.

We have to be able to access both ends (front and back) of the queue, and both ends can move. Therefore we should have two counters, one telling us where the front is, and one telling us where the end is. A third variable counting how many entries are in the list also simplifies this.

const int size=100;

class Queue

{ protected:

int front, back, num;

Person *data[size];

public:

Queue(void);

int is_empty(void);

void insert(Person *p);

Person *remove(void); };

Queue::Queue(void)

{ front=0;

back=0;

num=0; }

int Queue::is_empty(void)

{ return num==0; } // see how useful the third variable is?

void Queue::insert(Person *p)

{ if (num>=size) error(“insert when the queue is full”);

// insertions happen at the back:

if (back>=size) error(“oh dear”);

data[back]=p;

back+=1;

num+=1; }

Person *Queue::remove(void)

{ if (num==0) error(“remove when the queue is empty”);

// removals happen at the front:

if (front>=size) error(“oh dear”);

Person *answer=data[front];

front+=1;

num-=1;

return answer; }

The only problem with this solution is pointer out by the two “oh dear” errors. If we insert a Person into the queue, then immediately remove it, both counters, front and back, will have been increased by one, even though the queue remains empty. If this procedure is repeated 100 times, we will run out of space in the array, when the queue is empty of data.

One possibility is that every time a Person is removed from the queue, all remaining persons are moved up by one position, so that the value of front is always zero (of course we wouldn’t bother with the variable in that case). This works, but is terribly inefficient. In a large queue, all that moving could take more time than all the rest of the program.

There is a better method. Whenever front or back reach 100, reset them to zero (so the positions are really stored modulo size). So long as the back of the queue doesn’t catch up with the front (this is guaranteed not to happen if we keep track of num and never let the queue get full), we will never have a problem.

Under this scheme, insert and remove are changed as follows:

void Queue::insert(Person *p)

{ if (num>=size) error(“insert when the queue is full”);

// insertions happen at the back:

data[back]=p;

back+=1;

if (back==size) back=0;

num+=1; }

Person *Queue::remove(void)

{ if (num==0) error(“remove when the queue is empty”);

// removals happen at the front:

Person *answer=data[front];

front+=1;

if (front==size) front=0;

num-=1;

return answer; }

How would you change your definitions if there is no limit to the number of objects that may be in the queue at the same time? You do not need to re-write the whole answer, just indicate the changes that would be made.

This clearly requests a growable or resizable array. For this to work, data needs to be a pointer to an array instead of a direct array, and the constructor becomes responsible for creating the array. Also, size must become a variable in order to correctly record the current size.

As we are planning on changing the size of the array at some time, it would seem sensible to provide a method for doing this. I’ll make it protected so that users can’t play around with it.

class Queue

{ protected:

int front, back, num, size;

Person **data;

void resize(int newsize);

public:

Queue(void);

int is_empty(void);

void insert(Person *p);

Person *remove(void); };

Queue::Queue(void)

{ front=0;

back=0;

num=0;

size=100;

data = new (Person *) [size]; }

int Queue::is_empty(void)

{ return num==0; }

The insert method is only different when the array needs to grow, and the remove method doesn’t need to change at all. Notice how little the whole thing has had to change.

void Queue::insert(Person *p)

{ if (num>=size)

resize(size+100);

data[back]=p;

back+=1;

if (back==size) back=0;

num+=1; }

Person *Queue::remove(void)

{ if (num==0) error(“remove when the queue is empty”);

// removals happen at the front:

Person *answer=data[front];

front+=1;

if (front==size) front=0;

num-=1;

return answer; }

Now, the only major change is the addition or the resize method. Resize must create a new array of the appropriate size, and copy all the Person pointers into it. This would be an ideal time to tidy things up and make everything start from position zero again. It isn’t necessary to do this tidying up, but it certainly simplifies the procedure:

void Queue::resize(int newsize)

{ if (newsize<size) error(“somebody has messed up”);

Person **newdata = new (Person *) [newsize];

int oldpos=back, newpos=0;

for (int i=0; i<num; i+=1)

{ newdata[newpos] = data[oldpos];

newpos+=1;

oldpos+=1;

if (oldpos>=size) oldpos=0; }

delete[] data;

data=newdata;

size=newsize;

back=newpos;

front=0; }

A little complex perhaps, but it was an extra-credit part.

3.

A Dog is a special mammal for fetching sticks and eating things. It has a mouth at one end, a tail at the other end, and a leg at each corner. Draw a picture of a dog.