EEN118 LAB SIX
This lab is intended to reinforce what you have already learned and give more experence with the orderly design of useful programs. The result is a program that could be genuinely useful for engineering students.
You will need to download a new version of library.h and library.cpp before starting. Version 1.04.005 or later is required.
Plotting a Graph
Write a program that creates a graphics window 400 pixels wide and 400 pixels high. Draw inside it a graph of the function
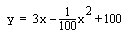
by designing a loop that varies x from 0 to 399, at each step calculating the appropriate value for y , and plotting a point at coordinates (x,y) . Remember that computer graphics systems make graphs come out upside-down. Your graph should look very much like this:
Making it Smoother
For most of the graph, the points are sufficiently close together for it to look like one continuoue smooth line, but near the ends you can see it degenerating into a disconnected series of dots. Modify your program so that it draws lines between the dots instead of single dots. Make the lines be bright red, and make sure there is no extraneous line between the pen's starting position and the leftmost point of the graph.
Horizontal (x) Scaling
Not every graph fits a 400×400 window quite so perfectly. For example, if you plot the graph of
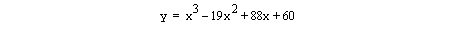
on the same axes, all the interesting part would be squashed up at the left-hand edge. The interesting part of that function is between x =0 and x =14.
Modify your program so that the value of x varies between 0 and 14, but it still occupies the whole window. Each pixel will now be worth a lot less x than it used to be worth, so you will have to do some scaling. Make sure you still plot a point for every pixel in the x direction, don't just plot 14 points. We want a nice smooth graph, looking a lot like this:
User-Controlled Horizontal (x) Scaling
Of course, the numbers 0 and 14 for the minimum and maximum values of x work out nicely for that graph, but should not be expected to be generally useful. Modify your program so that it asks the user for the minimum and maximum values of x before starting the plot, and uses the values entered instead of 0 and 14. This will be an absolutely trivial 1-minute change if you made a nice clean original design. If you didn't, I hope this teaches you the lesson!
Finding Extreme Values
It is often useful to know the maximum and minimum values that y can have. Modify your program so that while plotting the graph, it keeps track of the maximum and minimum values for y ever attained. Make it print them out as normal text output for the user to see. For the graph shown above running between x =0 and x =14, the minimum y is nearly 40, and the maximum is just over 300. Do not use calculus to work out what the minimum and maximum should be, make your program record what they actually are.
Vertical (y) Scaling
Now we will make use of the newly discovered information. Modify your program so that it works out the minimum and maximum values of y before starting to plot the graph. The easy way to do this is to duplicate the main loop in the program you have already got, so there are now two copies of it, one after the other. Remove all the graphics function calls from the first copy, so now all it does is work out all the y values and remember the minimum and maximum. Remove the min and max finding from the second copy, and you're there. Check that the program is still working at this point.
Now make your program use its knowledge of the minimum and maximum y values to do automatic vertical scaling, so that the minimum y value is plotted at the very bottom of the window, and the maximum at the very top. There should be no wasted space in the window.
If the conversion is difficult to work out, the Lab Guy is prepared with the formula. Don't be afraid to ask.
Your new graph should look like this, if x ranges between 0 and 14:
FOR EXTRA CREDIT ONLY
Make the window a little larger than it needs to be, so that you can draw axes and some indication of scale. Make it so that the program produces a nice professional looking graph that you could proudly turn in for a mathematics assignment. Both axes (i.e. the lines representing x=0 and y=0) should be shown and labelled (if they are within the visible ranges of x and y), faint grid lines should be drawn, indicating the scale, and the maximum and minimum should be clearly labelled. As usual for extra credit parts, use your imagination and make the results look good, without making your program get ugly or complicated.