Discs
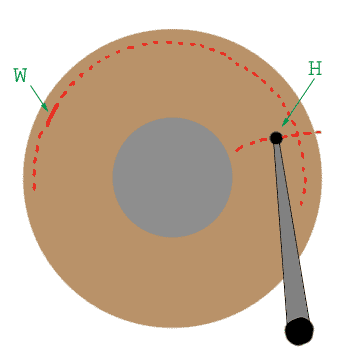

If the data wanted is at the position marked W, and the
read/write heads are currently at the position marked H,
the access time is easy to calculate. The disc needs to rotate
through the right angle, and the heads need to move to the right
track. For a random access, the average time will be the time
for half a rotation (= the Rotational Latency) plus the
track-to-track seek time.
The speed of rotation for a disc is usually heavily advertised.
If we take 7200 R.P.M. as an example, that means 120 revolutions
per second, or one revolution in 8.3 mS, for a rotational latency
of 4.1 mS.
The track-to-track seek time is less clear. The time to move the heads by a small
number of tracks is usually quite a bit less than the time to move the
heads right across the disc's surface, but it is not a linear relationship.
Moving the heads by one track is probably no faster than moving the heads
by 20 tracks. Usually we give the manufacturers the benefit of the doubt and
take the published track-to-track seek time as the average, but such a
plan is not always correct. Sometimes the "full stroke" seek time is nearly
ten times as long as the single track seek time. However, if disc
defragmentation and compaction is performed, it is quite likely
that each block accessed is quite close to the previous block accessed,
so the track-to-track seek time is not totally unreasonable. Typically,
this might be 3mS.
That gives an average access time of about 7mS for a modern disc drive,
but with a lot of caveats.
Until recently it was safe to assume that there would always be 63 blocks
around each track. Now the number is likely to be higher, but for the purposes
of estimations, using numbers like 63, 64, or 100 is quite reasonable.
If a program needs to read 25,252 bytes from a file, that will occupy 50
blocks (50*512=25600). If no special care is taken to allocate blocks in
an orderly way, that will require 50 random disc accesses, for a total of
350mS. However, if those 50 blocks are all on the same track, it is
only necessary to move the heads to that track, then in the worst case, read
that whole track, for an access time of about 10mS. Taking care to ensure
that consecutive blocks in a file are also consecutive blocks on one
track of a disc can speed up disc accesses by a factor of 50 or more.
To refer uniquely to a byte of data on a disc, it is necessary to specify
four things:
- Which surface (a disc can have more than 2),
- Which track on that surface (= which cylinder),
- Which block in that track (= which sector), and
- which byte in that block.
As the minimum acessible unit is a block (it is not possible to read or
write a single byte on disc), the fourth number is not of interest to the
file system. The other three can be compressed into a single unique
integer: (which surface) * (number of cylinders) * (number of sectors)
+ (which cylinder) * (number of sectors)
+ (which sector)
This number (called the or Address)
completely identifies any block on a particular disc. A file
system refers to places on disc by their block numbers.
Disc Formats
Each disc (or each partition of each disc) needs to be set-up correctly
before it can be used. There are generally four essential regions on
a disc (or partition):
- All of the essential parameters that can't be found out from the hardware,
such as the partitions name and any protections that apply to it, the cluster size
(if clusters are used), and the positions and sizes of the other three regions,
need to be stored in some fixed place. Typically block 0 of each partition is
set aside for storing these parameters.
- The Free-List, or File-Allocation-Table (or whatever scheme is in use):
when creating or extending files, it is essential to be able to find a new
block that is not already in use for some other purpose. The free list is
really just a list of block numbers. When a partition is formatted, the
numbers of all the free blocks are written, in order, in the free list. Whenever
a new block is needed, a number is taken from the free list. Whenever a block is
realeased (through deleting or shortening a file) its number is added back to
the free list.
If we have a 40GB disc, that means 80M blocks; it takes 4 bytes to store a block number,
so the free list will occupy 320M bytes, which requires 640K blocks. If a true
free-list system is used, on a 40GB disc, 655360 blocks will be occupied by the free list.
That sounds like a lot, but it is less than 1% of the total disc capacity.
- The root directory: Directories are just normal files that happen to contain
the names and addresses (block numbers) of other files; they are nothing special.
Except that the root directory has to be in some known place, so often it is not
really stored as a regular file within the file system. The root directory may
consist of a small number of blocks in a pre-determined place on the disc.
- The usable region for files.
Formatting a disc consists of setting up these four essential structures on the
disc (nothing has to be done to set up the usable region for files, and that
is by far the largest. Except that it is often considered prudent to test every
block before it is used. The formatting process might check that each usable
block really is correctly functioning before adding its number to the free list.
This can make formatting take a very long time.)
The Free List
The free list just contains the block number of every block that is still available for use.
It has to be kept on disc partly because it is very big, and partly because it
is permanent information. When a computer is switched off, its file system
should survive.
This causes trouble. The free list can not be entirely disc resident, because then
every tiem a block is needed or released, two extra disc accesses will be needed
(one to read information from the free list, and one to write back the modified
portion of the free list). This would slow down all file operations too much
to be acceptable.
As the free list is much too big to keep entirely in memory, just part of it is
kept in memory, with the rest left on the disc. The free list behaves like a stack,
so only the top (active) portion needs to be kept in memory. Typically when the operating
system is started, it might read 100 blocks of free block numbers from the free list
into memory. As blocks are used or released, only the memory-resident portion is
changed. If so many blocks are allocated that the memory-resident "window" is exhausted,
it is easy to read a further portion from the disc. Similarly, if so many files are
deleted that the memory-resident window gets over-full, it can easily be dumped onto
the disc to make more space. The O.S. just has to be careful that the memory-resident
window is always saved to disc.
Files
A sensible operating system does not attempt to store all information about a file
in directories. There is just too much important information: file name (can be long),
dates (creation, last modified, last backed-up), owner, protections, file-type,
perhaps even a comment about what the file is, and who-knows-what-else. DOS tries
to store evrything in the directory, and as a result almost nothing is known about
DOS files.
Every file should have one representative block that stores all of the important information
about that file, and somehow ties it all together. This representative block is called the
Header Block. Directory entries only need to contain a file's name and the
address of its header block. In fact, even the name can be left out of the directory,
but that can result in directory listings taking a long time to produce.
The useful information about a file is very unlikely to fill a whole block, so there
is normally plenty of space left over in the header block for other things. This is
how the whole file is tied together. For the sake of examples, I always assume that
there are 112 byte's worth of useful information to be recorded about a file, leaving
400 bytes for administrative purposes. That gives enough space for a nice round
100 pointers to other blocks.
Two possible file formats immeiately present themselves. For really small files
(less than 401 bytes of real data) the pointer space in the header block can
be used for direct data storage. This results in very efficient use of disc space,
but for some unfathomable reason is hardly ever used in real operating systems.
The other possibility is that
the 400 bytes are used to store the addresses of the blocks that contain the actual
data. Each block has room for 512 bytes, and we have room for 100 pointers, so
(under the stated assumptions) this file format (called a Single Level Index)
has a maximum capacity of 51,200 bytes. Not very big, but a reasonable start.
A Two Level Index file also has up to 100 pointers to other disc blocks in its
header, but each of those blocks contain northing but pointers to other blocks, and
it is those other blocks that contain the data. This gives room for 100 pointers
to pointer blocks, each pointer block has room for 128 pointers to data blocks, and
each data block as always has room for 512 bytes. A two level index file therefore
has a maximum capacity of 100*128*512 = 6,553,600 bytes. Much better, but still
not enough for a modern system.
Naturally, there can also be a three level index file, with 100 pointers in the header,
each leading to a block of 128 pointers, each leading to another block of 128 pointers,
each leading to a block of 512 bytes of data, for a maximum capacity of 838,860,800 bytes.
Similarly, a four level index file would have a maximum capacity of 107,374,182,400.
Under unix-like systems, a compromise format, based on I-nodes is used. An I-node
is what unix uses as a header blcok for a file, so every file is represented by an I-node.
the 400 pointer bytes are divided up into three of four regions of possibly different sizes.
For the putposes of this example, I will assume four equally sized regions of 25 pointers
each. In the first region, the 25 pointers point directly to data blocks. In the second region,
the 25 pointers point to pointer blocks, each containing 128 pointers to data blocks.
In the third region, the 25 pointers point to pointer blocks, each of which contains 128 pointers
to other pointer blocks, each of which contains 128 pointers to data blocks. The fourth
region follows the same pattern. This gives a maximum capacity of 25x512 + 25x128x512 + 25x128x128x512
+ 25x128x128x128x512 = about 26.8 GB. Remember that the total capacity can be adjusted by
changing the sizes of the four regions, or even adding or removing a region.
Access Speed
Why not just use the format that gives the best maximum capacity? Because that format also
gives the worst access time. It is possible for an operating system to support multiple
file formats (it just needs one byte in the header to indicate which format is currently in
use for this file). Most modern operating systems don't bother to do this. Unix uses the
I-node because it gives a reasonable compromise for little extra effort.
When considering the access time, it is important to think of three things:
- The time taken to open a file and read the first byte,
- The time taken to read the next byte in sequence, and
- The time taken to read a random byte from anywhere in the file.
We'll work it all out for a one-level index file as an example; the others can be
worked out in the same way. As we have not thought much about exactly what a directory
looks like, we will not worry about the time taken to find a file in the directory
(it is not really a function of the file format anyway), and just start the timing from
when we already know the block number of the file's header block.
- Getting the first byte: Two disc accesses: one to read the header and its 100 pointers,
then one to read the first data block. Using the previously made assumptions, this comes
to 14mS.
- Getting the next byte: Once the first byte has been read, the next 511 bytes are
automatically available for free (a whole block has to be read at once), it is only after
512 bytes have been read that another block has to be read. So the average time to get
the next byte in sequence is one disc access time divided by 512 bytes, or 14 micro-seconds.
- Getting a random byte: Taking a simple view, as there are up to 100 blocks in the
file, there is a 1% chance that the random byte wanted will be in the same block as the last
byte wanted and therefore not require another read, and a 99% chance that it will be in a different
block and therefore require one disc access time. But not all files will be of the maximum size,
so the 99% figure could be reduced by a large amount. However, it is not until we start dealing
with very small files that it makes any appreciable difference to the final result, so we
can (almost) safely disregard the possibility of not needing a new disc access. The time for
a random byte to be read is 7 milli-seconds.
When calculating the times for larger file formats, the same principles are used, but remember
that memory is not as expensive as it used to be. With a two-level index, it could be considered
reasonable to read all 100 of the pointer blocks into memory when they are first needed, and
keep them permanently in memory until the file is closed. That would only take 51K of memory, and would only be done when
random access is required (not very common), so would be a minimal expense, that would result
in the average random access time being halved.
It is even possible to do the same for a three-level index. Even though there could be up to
12,800 pointer blocks, requiring a total of 6.4MB to keep them memory-resident, it is something
that would only be done when random access of a giant file is being performed very frequeuntly
and needs maximum speed. In such rare cases, the ability to effectively speed up disc accesses
by a factor of 3 could easily be worth 6MB of ram.
So we can see that as a general rule, access times get longer as the maximum capacity of a file
format gets larger. It is also clear that the efficiency for smaller files is similarly reduced.
The smallest possible file using a one level index occupies 2 blocks. The smallest possible
with a four level index requires 5 blocks, so a single byte of data on disc could occupy
2560 bytes of disc space. This is why supporting multiple formats is good, and unix's I-node
is a reasonable compromise. Using I-nodes, small files behave like single level indexes,
it is only when the file size exceeds 12,800 bytes that the second region of pointers needs
to be used, and it starts to behave like a two level index: you only pay the penalty in
performance when you need increase in capacity.
Note:
When calculating capacities and other things, a calculator is hardly ever needed. the number
of bytes in a block, 512, is 2 to the power of 9 (2^9). The number of pointers in a pointer
block is 2 to the power of 7 (2^7), so the maximum capacity of a four level index file
is 100 x 128 x 128 x 128 x 512, or 100 x 2^7 X 2^7 x 2^7 x 2^9, whish is 100 x 2^(7+7+7+9)
or 100 x 2^30. Everyone can multiply by 100 easily, and everyone should be able to do two-to-the-power-ofs easily.
Just remember that 2^10 is very close to 1,000 so 2^30 is very close to 1,000,000,000.
So the capacity of a 4 level index file is very close to 100,000,000,000 bytes, or 100GB, without
needing a calculator.

