Heaps

A heap is a binary tree with a special ordering imposed upon it. Every item or node in the heap has a priority associated with it, and the priority determines where a node as allowed to be, with respect to the other nodes.

There is a special node, called the "root", which forms the base of the heap. Every node except for the root has a "parent", which is directly above it. If A is the parent of B, then B is a child of A. Every node has zero, one, or two children, never more.

The ordering rule is very simple. For a "Min-Heap", the most common form, the only rule is that no node's priority may be less than its parent's priority. For a "Max-Heap", no child may be greater than its parent. Remember that the usual scheme is to have numerically low priorities correspond with high degrees of importance or urgency, so in a Min-Heap, the most important node is at the top.

That is it. No global rules, just every node >= its parent.

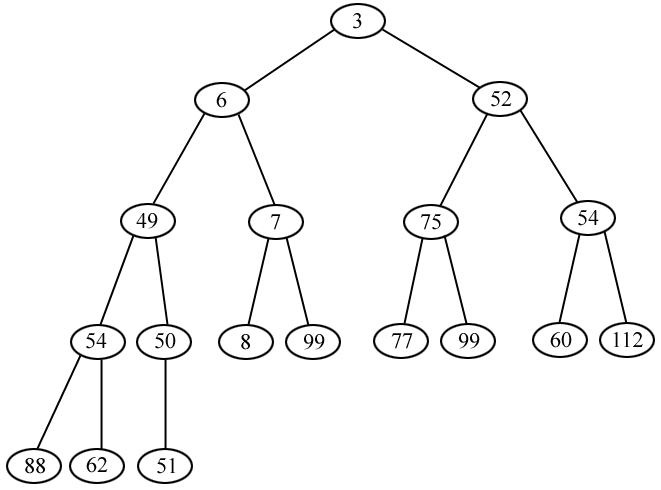
Here is a perfectly healthy and happy heap. Observe that it follows the rules. Even though a little number like 8 is way down at the 4th level, when something big like 52 is at the second level, the rule "every node is >= its parent" is always strictly obeyed. Nothing else matters.



The other thing that makes heaps interesting is that they happily live inside arrays. If you have a heap with up to N items in it, then an array with indexes ranging from [1] to [N] is just perfect for representing it, contents plus structure. (C and C++ insist that arrays start at [0], so you need N+1 elements). The plan is that the root is always at index [1]. For any node at index [X], its parent is at index [X/2], and its (up to) two children are at indices [2X] and [2X+1]. Here is the example heap from the above diagram living in an array:
1:  3
2:  6
3:  52
4:  49
5:  7
6:  75
7:  54
8:  54
9:  50
10:  8
11:  99
12:  77
13:  99
14:  60
15:  112
16:  88
17:  62
18:  51
Laid out like that, you can easily see that a heap isn't properly sorted in the normal sense, but it is a little bit sorted. Making a heap is half way to sorting an array.

I think it is easier to understand a heap if you draw the array differently. The following shows exactly the same array, making exactly the same heap, but it manages to show both layouts at the same time.
1:  3
2:  6
3:  52
4:  49
5:  7
6:  75
7:  54
8:  54
9:  50
10:  8
11:  99
12:  77
13:  99
14:  60
15:  112
16:  88
17:  62
18:  51
19:  
20:  
21:  
22:  
23:  
24:  
25:  
26:  
27:  
28:  
29:  
30:  
31:  
There are only three things you can reasonably do with a heap: remove a node from it, add a node to it, or reposition a node that is already in it.

The Three Operations

The object of happy heap manipulation is to minimise disruption. Always do everything in the easiest possible way.

Insertion

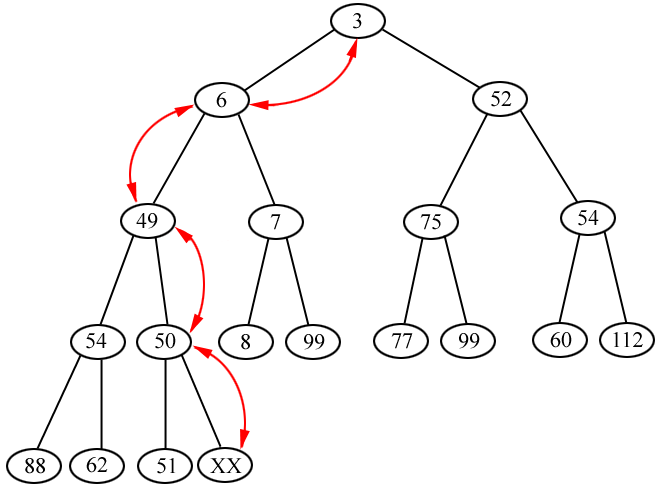
If you want to insert a new piece of data with minimal disruption, just look at the above diagram, and you'll see that putting it in the first free space (in this case index [19]) is the only option that doesn't require moving around items that are already properly in place. Of course, putting new data at position [19] might violate the one heap rule, but that is easy to fix. Let's call the value we are inserting "XX", and see what the heap looks like if we put it at the first free space:
1:  3
2:  6
3:  52
4:  49
5:  7
6:  75
7:  54
8:  54
9:  50
10:  8
11:  99
12:  77
13:  99
14:  60
15:  112
16:  88
17:  62
18:  51
19:  XX
20:  
21:  
22:  
23:  
24:  
25:  
26:  
27:  
28:  
29:  
30:  
31:  
The only rule for a heap is in terms of a node's relationship with its parent, so we'll look at how XX (at index [19]) relates to its parent (at index [9]). (Why [9]? The parent of [N] is at [N/2], and of course these are integer operations, 19/2 is 9). The Va;ue in the parent node is 50.

There are only two cases:

Depending on how small XX is, it could work its way all the way to the top of the tree. This diagram shows what could happen. XX is added, and keeps getting compared with its parent, swapping if necessary. As soon as the item finds itself in a valid position (either >= its parent, or at the root of the heap), the procedure stops.

Here is the insertion procedure: 
      void insert(data xx)
      { N+=1;
        heap[N]=xx;
        fix_upwards(N); }

      void fix_upwards(int position)
      { while (true)
        { if (position==1) break;
          int parent=position/2;
          if (heap[position].priority >= heap[parent].priority) break;
          swap(heap[position], heap[parent]);
          position=parent; } }




Removal

Of course, we could remove any item from the heap, but we want to keep it simple. The only thing we are likely to want to remove is the top thing. Heaps have no overall ordering, the only overall position we can rely on is that the smallest (most important) thing will be at the top. The top is the only item that matters, so the top is the only one we are likely to really want to get our hands on.

Removing the top item would completely destroy the heap, so we'd like to avoid it. In fact, the only item that is easy to remove is the very last one, the 51 at position [18]. So we make a compromise. We'll swap the one we want (item [1]) with the one that is easy to remove (item [18]), then remove the easy one.

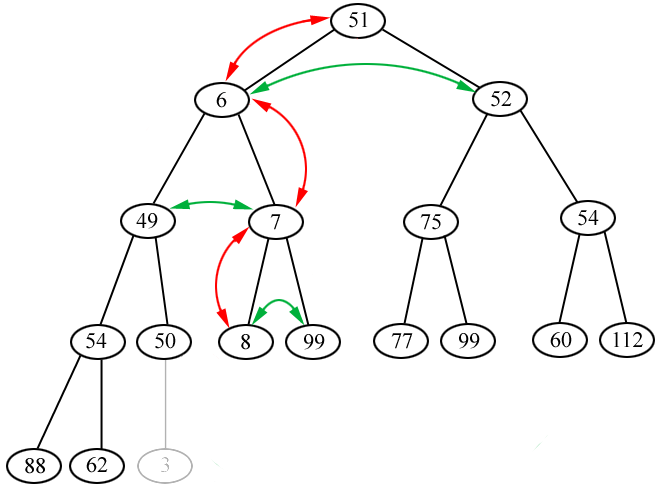
This results in the following heap configuration (ignore the coloured arrows for now). We've got the 3 from the top, and put the 51 in its place. Of course, the heap is not healthy any more, it has a bif number at the top, but the repeairs are quite easy.

The 3, which appears in ghostly grey at the end, isn't really in the heap any more. Just subtracting 1 from N tells us not to look at that item. The only thing that has moved is the 51 now at the top. As the heap was OK before the move, the only possible problem is that the 51 (at index [1]) might have a child (at indices [2] and [3]) that is smaller than it. So what we do is find out whether that really is the case. If it isn't, then the heap is still good, there is no fixing to do. If the root is not the smallest any more, then we need to do something.

If the item now at the top isn't the most important in the whole heap, then one of its direct children (6 or 52) must be. It is easy to find out which (compare them and take the smallest). So the new, out-of-place, root is swapped with its smallest (most importand) child. After the swap, it still might be out of position, so we continue the checking. Keep track of where the out-of-place item is, if it is > any of its children, swap it.

This diagram shows the procedure. The read arrows show the progress of the displaced 51, being compared with its children and swapped with the smallest. The green arrows show the two children being compared to see which wins.



Here is the whole procedure for taking the most important item out of the heap, then repairing the heap. 
      data remove(void)
      { swap(heap[1], heap[N]);
        N-=1;
        fix_downwards(1);
        return heap[N+1]; }

      void fix_downwards(int position)
      { while (true)
        { int left_child = position*2;
          int right_child = left_child+1;
          if (left_child > N) break;
          int best_child = left_child;
          if (right_child <= N)
          { if (heap[right_child].priority < heap[left_child].priority)
              best_child = right_child; }
          if (heap[position].priority < heap[best_child].priority) break;
          swap(heap[position], heap[best_child]);
          position = best_child; } }

Priority Change

Happily, there is nothing to think about here. If the priority of an item already in the heap is changed, there are only two possibilities. If it gets less important, then it might need to be replaced by one of its children. If it gets more important then it might need to replace its own parent. We have already worked out how to do both of those things: 
      void adjust(int position, int new_priority)
      { int old_priority = heap[position].priority;
        heap[position].priority = new_priority;
        if (new_priority < old_priority)
          fix_upwards(position);
        else
          fix_downwards(position); }



And that is just about all that could possibly be said about the mechanics of heap operations.